Answer:
![\boxed{\begin{aligned}f(g(x))&=f\left(\sqrt[3]{5x}\right)\\&=x\end{aligned}}](https://img.qammunity.org/2024/formulas/mathematics/college/hv8yr5fo1qxts1lwkpbjjz59ao77gfcyfh.png)
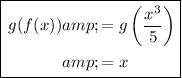
The graph of f is the reflection of the graph of g in the line y = x.
Explanation:
To show that two functions are inverses, we need to show that:
- f(g(x)) = x, for all x in the domain of g(x), and
- g(f(x)) = x, for all x in the domain of f(x).
Given functions:
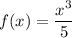
![g(x)=\sqrt[3]{5x}](https://img.qammunity.org/2024/formulas/mathematics/college/e4pt6rcnwnwmyqoxbz3nrzs1t75kzdr0vt.png)
Find f(g(x)) by substituting x = g(x) into f(x):
![\begin{aligned}f(g(x))&=f\left(\sqrt[3]{5x}\right)\\\\&=\frac{\left(\sqrt[3]{5x}\right)^3}{5}\\\\&=\frac{\left((5x)^{(1)/(3)}\right)^3}{5}\\\\&=(5x)/(5)\\\\&=x\end{aligned}](https://img.qammunity.org/2024/formulas/mathematics/college/zwne5k0rylmzhr2onf64qqx23jjk1w3i96.png)
Find g(f(x)) by substituting x = f(x) into g(x):
![\begin{aligned}g(f(x))&=g\left((x^3)/(5)\right)\\\\&=\sqrt[3]{5\left((x^3)/(5)\right)}\\\\&=\sqrt[3]{x^3}\\\\&=(x^3)^{(1)/(3)}\\\\&=x\end{aligned}](https://img.qammunity.org/2024/formulas/mathematics/college/drrhz0q9xr03yh57u196qn1n0k5mce5j5w.png)
Therefore, as f(g(x)) = x and g(f(x)) = x, we have successfully demonstrated that f(x) and g(x) are inverses.
If we graph the two functions (see attached), we can see that:
- The graph of f is the reflection of the graph of g in the line y = x.