Question

Solve the quadratic by factoring. 2x²+4=3x+9

Answer 1

Hello!

Answer:

`\Large \boxed{\sf x_1 = (5)/(2)~~ ,~~ x_2 =-1}`

Explanation:

→ We want to solve this equation by factoring:

`\sf 2x^2+4=3x+9`

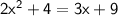
→ Put the equation to 0:

◼ Subtract 9 from both sides:

`\sf 2x^2+4-9=3x+9-9`

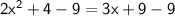
◼ Simplify both sides:

`\sf 2x^2-5=3x`

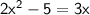
◼ Subtract 3x from both sides:

`\sf 2x^2-5-3x=3x-3x`

◼ Simplify both sides:

`\sf 2x^2-3x-5=0`

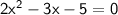
→ It's a quadratic equation because it's on the for ax² + bx + c = 0.

→ To solve a quadratic equation, we can:

- solve with the quadratic formula

- solve by factoring

→ We want to solve by factoring, so, let's factorize the equation:

`\sf 2x^2+2x-5x-5=0`

`\sf (2x^2+2x)+(-5x-5)=0`

`\sf 2x(x+1)-5(x+1)=0`

`\sf (2x -5)(x+1)=0`

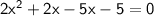
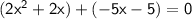
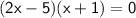
→ Now, we have the two equations:

`\sf 2x-5=0`

`\sf x+1=0`

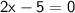
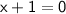
→ Let's solve these two equations to find the two solutions of the equation:

First solution:

→ We want to solve this equation to find the 1st solution of our equation:

`\sf 2x-5=0`

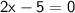
◼ Add 5 to both sides:

`\sf 2x-5+5=0+5`

◼ Simplify both sides:

`\sf 2x=5`

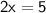
◼ Divide both sides by 2:

`\sf (2x)/(2) = (5)/(2)`

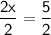
◼ Simplify both sides:

`\boxed{\sf x = (5)/(2)}`

Therefore, the first solution of our equation is 5/2.

Second solution:

→ We want to solve this equation to find the 1st solution of our equation:

`\sf x+1=0`

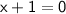
◼ Subtract 1 from both sides:

`\sf x+1-1=0-1`

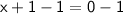
◼ Simplify both sides:

`\boxed{\sf x = -1}`

Therefore, the second solution of our equation is -1.

Conclusion:

The solutions of the equation 2x² + 4 = 3x + 9 are 5/2 and -1.