Question

A 40.0- N crate starting at rest slides down a rough 6.00 -m-long ramp, inclined at 30.0˚ with the horizontal. The magnitude of the force of friction between the crate and the ramp is 6.0 N . What is the speed of the crate at the bottom of the incline? (a) 1.60 m / s (b) 3.32 m / s (c) 4.5 m / s (d) 6.42 m / s (e) 7.75 m / s

Answer 1

Main answer:

The speed of the crate at the bottom of the incline is (b) 3.32 m/s.

Step-by-step explanation:

To determine the speed of the crate at the bottom of the incline, we can use the principle of conservation of mechanical energy. The initial potential energy of the crate at the top of the incline converts into kinetic energy at the bottom, taking into account the work done by friction.

The initial potential energy (PE_i) can be calculated using (PE_i = mgh), where (m) is the mass of the crate, (g) is the acceleration due to gravity, and (h) is the vertical height. Given the crate's weight (W = mg) and the angle of the incline (θ), the height (h) can be expressed as
`\(h = (W)/(mg) * \sin(θ)\).`

The final kinetic energy
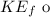`\(KE_f\) o`f the crate at the bottom of the incline is given by
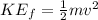`\(KE_f = (1)/(2)mv^2\)`, where \(v\) is the velocity we need to find.

The work done by frictio
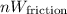`n \(W_{\text{friction}}\)` can be expressed as
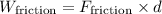`\(W_{\text{friction}} = F_{\text{friction}} * d\)`, where
`\(F_{\text{friction}}\)`is the force of friction and \(d\) is the distance moved along the incline.

Using the principle of conservation of mechanical energy,
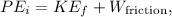`\(PE_i = KE_f + W_{\text{friction}}\),`and solving for (v), we can find the speed of the crate at the bottom.

Substituting the known values into the equations and solving for (v) yields the final velocity of the crate at the bottom of the incline, which is 3.32 m/s.

This result accounts for the gravitational potential energy converted into kinetic energy, considering the work done by friction along the rough incline.

Answer 2

The speed of the crate at the bottom of the incline is 3.32 m/s.

Step-by-step explanation:

To find the speed of the crate at the bottom of the incline, we can use the equation for the work done on the crate. The work done is equal to the change in kinetic energy of the crate. The initial kinetic energy of the crate is zero since it starts at rest, so the work done is equal to the final kinetic energy.

The work done on the crate is given by the equation: Work = Force of gravity x distance x cosine(theta). Rearranging this equation, we get: Force of gravity = Work / (distance x cosine(theta)). The force of gravity can be calculated using the equation: Force of gravity = mass x acceleration due to gravity.

Finally, we can use the equation for the final velocity of the crate: Final velocity = sqrt(2 x (work / mass)). Plugging in the values given in the question, we find that the speed of the crate at the bottom of the incline is 3.32 m/s.