Question

Please find the general limit of the following function:


`\lim_(x \to 9)(x^2 + 2^7 + (9.1 * 10))`

Answer 1

Explanation:

Hey there!

Please look your required answer in picture.

Note: In left hand limit always take a smaller near number of the approaching number. For example as in the solution I took the 8.99,8.999 as it is smaller than 9 but very near to it.

And in right hand limit always take a smaller and just greater near number than the approaching number. For example, I took 9.01,9.001 which a just greater but very near to 9.

Hope it helps!

Answer 2

The general limit exists at x = 9 and is equal to 300.

Explanation:

We want to find the general limit of the function:

`\displaystyle \lim_(x \to 9)(x^2+2^7+(9.1* 10))`

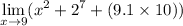
By definition, a general limit exists at a point if the two one-sided limits exist and are equivalent to each other.

So, let's find each one-sided limit: the left-hand side and the right-hand side.

The left-hand limit is given by:

`\displaystyle \lim_(x \to 9^-)(x^2+2^7+(9.1 * 10))`

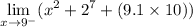
Since the given function is a polynomial, we can use direct substitution. This yields:

`=(9)^2+2^7+(9.1* 10)`

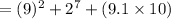
Evaluate:

`300`

Therefore:

`\displaystyle \lim_(x \to 9^-)(x^2+2^7+(9.1 * 10))=300`

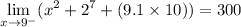
The right-hand limit is given by:

`\displaystyle \lim_(x \to 9^+)(x^2+2^7+(9.1* 10))`

Again, since the function is a polynomial, we can use direct substitution. This yields:

`=(9)^2+2^7+(9.1* 10)`

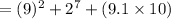
Evaluate:

`=300`

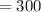
Therefore:

`\displaystyle \lim_(x \to 9^+)(x^2+2^7+(9.1* 10))=300`

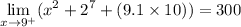
Thus, we can see that:

`\displaystyle \lim_(x \to 9^-)(x^2+2^7+(9.1* 10))=\displaystyle \lim_(x \to 9^+)(x^2+2^7+(9.1* 10))=300`

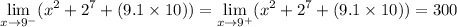
Since the two-sided limits exist and are equivalent, the general limit of the function does exist at x = 9 and is equal to 300.