Question

AWARDING 100 PTS FOR DIS!!!! I NEED HELPPP

Answer 1

`\textsf{1)} \quad (625)/(1296)`

`\textsf{2)}\quad 0.21\; \sf (nearest\;hundredth)`

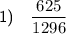
Explanation:

Question 1

Given expression:

`(\left(\left((6)/(5)\right)^5\right)^(-2))/(\left((6)/(5)\right)^(-6))`

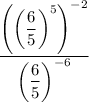
To simplify the given expression, we can use the following laws of exponents:

`\boxed{\begin{array}{rl}\underline{\sf Laws\;of\;Exponents}\\\\\sf Power\;of\;a\;Power:&(a^m)^n=a^(mn)\\\\\sf Negative\;Exponent:&a^(-m)=(1)/(a^m)\\\\\sf Product:&a^m * a^n=a^(m+n)\\\\\sf Power\;of\;a\;Quotient:&\left((a)/(b)\right)^m=(a^m)/(b^m)\\\\\end{array}}`

First, apply the power of a power law to the numerator:

`(\left((6)/(5)\right)^(5\cdot-2))/(\left((6)/(5)\right)^(-6))`

`(\left((6)/(5)\right)^(-10))/(\left((6)/(5)\right)^(-6))`

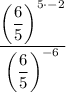
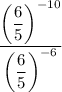
Apply the negative exponent law to the numerator:

`(1)/(\left((6)/(5)\right)^(10)\cdot\left((6)/(5)\right)^(-6) )`

Apply the product law to the denominator:

`(1)/(\left((6)/(5)\right)^(10+(-6)))`

`(1)/(\left((6)/(5)\right)^(4))`

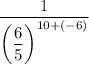
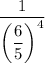
Apply the power of a quotient law to the denominator:

`(1)/((6^4)/(5^4))`

`\textsf{Apply the fraction rule} \quad (a)/((b)/(c))=(ac)/(b):`

`(1 \cdot 5^4)/(6^4)`

`( 5^4)/(6^4)`

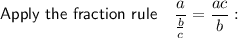
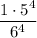
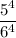
Finally, compute the numbers:

`\Large\boxed{\boxed{(625)/(1296)}}`

`\hrulefill`

Question 2

Given expression:

`\left(\left(1.3\right)^3\right)^(-2)`

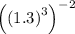
To simplify the given expression, we can use the following laws of exponents:

`\boxed{\begin{array}{rl}\underline{\sf Laws\;of\;Exponents}\\\\\sf Power\;of\;a\;Power:&(a^m)^n=a^(mn)\\\\\sf Negative\;Exponent:&a^(-m)=(1)/(a^m)\end{array}}`

First, apply the power of a power law:

`\left(1.3\right)^(3\cdot(-2))`

`\left(1.3\right)^(-6)`

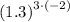
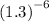
Now, apply the negative exponent law:

`(1)/(\left(1.3\right)^6)`

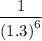
Compute 1.3⁶ using a calculator:

1.3⁶ = 4.826809

Rewrite this as a fraction:

`4.826809=(4826809)/(1000000)`

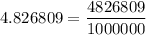
Therefore:

`(1)/(1.3^6)=(1)/((4826809)/(1000000))=(1000000)/(4826809)`

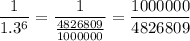
Using a calculator:

`(1000000)/(4826809)=0.207176211...=0.21\; \sf (nearest\;hundredth)`

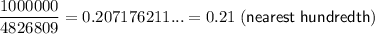
So, the simplified expression rounded to the nearest hundredth is:

`\Large\boxed{\boxed{0.21}}`

Answer 2

`\textsf{1st question:}\sf (625)/(1296)`

`\textsf{2nd question:} 0.21`

Explanation:

Before solving this:

We need to know the law of indices:

When power has the same base:

`\sf \begin{aligned} \textsf{ Multiplication law} &\sf : a^m * a^n = a^(m+n) \\\\ \textsf{Zeroth power rule} &\sf = a^(0) = 1\\\\ \textsf{Division law} &\sf : = (a^m)/(a^n) = a^(m-n) \\\\ \textsf{Negative power rule}&\sf : a^(-n) = (1)/(a^n) \\\\ \textsf{Power law}&\sf : (a^m)^n = a^(mn) \end{aligned}`

For 1st Question:

`\sf ( \left(\left((6)/(5) \right)^5\right)^(-2))/(\left((6)/(5) \right)^(-6))`

Using Power law:

`\sf ( \left((6)/(5) \right)^(5* -2))/(\left((6)/(5) \right)^(-6))`

`\sf ( \left((6)/(5) \right)^(-10))/(\left((6)/(5) \right)^(-6))`

Now, using Division law:

`\sf \left((6)/(5) \right)^(-10-(-6))`

`\sf \left((6)/(5) \right)^(-10+6))`

`\sf \left((6)/(5) \right)^(-4)`

In order to make a positive power, replace 6 by 5 and 5 by 6 or using negative power rule:

we get

`\sf \left((5)/(6) \right)^(4)`

Distribute the power:

`\sf (5^4)/(6^4)`

`\sf (625)/(1296)`

So, answer in the fraction is:

`\sf (625)/(1296)`

`\hrulefill`

For 2nd Question:

`\left((1.3)^3\right)^(-2)`

Using power rule:

`\sf (1.3)^(3* -2)`

`\sf (1.3)^(-6)`

Using Negative power rule:

`\sf (1)/(1.3)^6`

Using the calculator we can find the value:

`\sf (1)/(4.826809)`

`\sf 0.207176211`

In the nearest hundred:

`\sf 0.21`