Question

1) Point A is at (2, 2). Point B is at (-4,2).

Point B is on AC. The distance from B to C is
5.
What are the coordinates of C?
How long is AC?

Answer 1

Check the picture below.

Answer 2

Length of AC = 11 units

The coordinates of C = (-9, 2)

Explanation:

Given:

• Point A is at (2, 2) and Point B is at (-4, 2).
• Point B is on the line segment AC .
• Distance from B to C is 5.

To find:

• Coordinates of Point C
• The length of AC.

Solution:

Since the x coordinate is different in point A and B which becomes negative but y coordinate is constant.

so, we can say that:

Point C lies in second quadrant.

Therefore, x coordinate of C is -5 units far from x coordinate of B.

So,

Coordinate of C is (-4-5,2)=(-9,2)

Now,

let's find the length of AC.

We can use the distance formula to calculate the distance between points A and C:

The distance formula is a formula used to find the distance between two points in a coordinate plane. It is given by the following formula:

`\sf d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

where:

• d is the distance between the two points
• x1 and y1 are the coordinates of the first point (2,2)
• x2 and y2 are the coordinates of the second point(-9,2)

Substituting the coordinates of A and C:

`\begin{aligned} \textsf{Distance AC } &\sf =√((-9- 2)^2 + (2 - 2)^2)\\\\&\sf =√((-11)^2 + 0^2) \\\\&\sf =√(121)\\\\&\sf = 11 \textsf{ units}\end{aligned}`

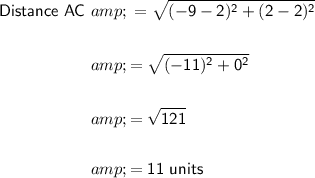
So, the length of AC is 11 units, and the coordinates of C is (-9, 2).