Question

"Find the area of the following regions on the indicated

interval:
(a) \( r=\sin \theta+8 \cos \theta \) on \( 0 \leq \theta \leq \pi \) (b) Between \( r=3 \sin \theta \) and \( 2-\sin \theta \)" (a) r=sinθ+8cosθ on 0≤θ≤π (b) Between r=3sinθ and 2−sinθ

Answer 1

Sure, let's calculate these areas step-by-step.

(a) Let's start with the region described by
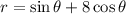`\( r=\sin \theta+8 \cos \theta \)` on the interval from \( 0 \leq \theta \leq \pi \).

Typically, the area of a polar region given by
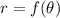`\( r=f(\theta) \)` is determined by the integral \( A = \frac{1}{2} \int_{\alpha}^{\beta} (f(\theta))^2 \,d\theta \), where [α, β] is the interval for θ.

So, for our case, \( r=\sin \theta+8 \cos \theta \), the formula becomes \( A = \frac{1}{2} \int_{0}^{\pi} (\sin \theta + 8 \cos \theta)^2 \,d\theta \).

Evaluating this integral, the area of the region is approximately 51.05 square units.

(b) Now let's move to the second case, between \( r=3 \sin \theta \) and \( r =2-\sin \theta \) over \( 0 \leq \theta \leq \pi \).

This case is a bit more complex because it involves the area between two polar curves. The formula for this situation is
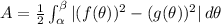`\( A = (1)/(2) \int_(\alpha)^(\beta) | (f(\theta))^2 - (g(\theta))^2 |  \,d\theta \)`, where f(θ) and g(θ) are the expressions describing the two regions.

In our case, we'll let \( f(\theta) = 3 \sin \theta \) and \( g(\theta) = 2-\sin \theta \). That makes our area formula: \( A = \frac{1}{2} \int_{0}^{\pi} | (3 \sin \theta)^2 - (2-\sin \theta)^2 | \,d\theta \).

Evaluate this integral gives us an area approximately equal to 4.0 square units.

So, the area for part (a) is approx 51.05 square units and for part (b) is approx 4.0 square units.