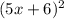Question

Decompose polynomials into factors:
a) x² + 6x - 2;
b) 25x² + 60x + 36;​

Answer 1

`\textsf{a)}\quad (x+3+√(11))(x+3-√(11))`

`\textsf{b)} \quad (5x+6)^2`

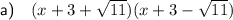
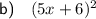
Explanation:

Decomposing polynomials into factors is a mathematical process of expressing a polynomial as a product of simpler polynomials or monomials. This involves breaking down a given polynomial into its constituent factors in such a way that when you multiply these factors together, you obtain the original polynomial.

`\hrulefill`

Question a)

Given polynomial:

`x^2+6x-2`

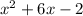
The given polynomial is a quadratic polynomial because the highest exponent of the variable x is 2.

Quadratic polynomials have the general form ax² + bx + c, where a, b, and c are constants. In this case, a = 1, b = 6, and c = -2.

We cannot factor this polynomial by grouping, since there are no factors of the product of
`a` and
`c` (-2) that sum to
`b` (6). Therefore, we can factor the polynomial by using the quadratic formula.

The quadratic formula is a method for finding the roots (or solutions) of a quadratic equation (which are the points where the corresponding parabola intersects the x-axis).

Once the roots have been found using the quadratic formula, we can use those values to factor the quadratic equation into its linear factors of the form (x - x₁)(x - x₂), where x₁ and x₂ are the roots.

`\boxed{\begin{array}{l}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when} \;ax^2+bx+c=0 \\\end{array}}`

Substitute a = 1, b = 6 and c = -2 into the quadratic formula to find the roots of the polynomial.

`x=(-6 \pm √(6^2-4(1)(-2)))/(2(1))`

`x=(-6 \pm √(36+8))/(2)`

`x=(-6 \pm √(44))/(2)`

`x=(-6 \pm √(2^2\cdot 11))/(2)`

`x=(-6 \pm √(2^2)√(11))/(2)`

`x=(-6 \pm 2√(11))/(2)`

`x=-3 \pm √(11)`

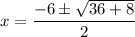
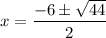
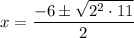
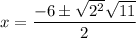
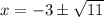
Therefore, the two roots are:

`x_1=-3-√(11)`

`x_2=-3+√(11)`

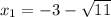
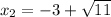
Substitute the two roots into the form (x - x₁)(x - x₂):

`(x-(-3-√(11)))(x-(-3+√(11)))`

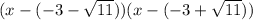
Simplify:

`(x+3+√(11))(x+3-√(11))`

`\hrulefill`

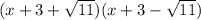
Question b)

Given polynomial:

`25x^2 + 60x + 36`

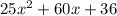
The given polynomial is a quadratic polynomial because the highest exponent of the variable x is 2.

Quadratic polynomials have the general form ax² + bx + c, where a, b, and c are constants. In this case:

• a = 25
• b = 60
• c = 36

To factor by grouping, we need to find two numbers that multiply to
`ac` and sum to
`b`.

The product of a and c is:

`a * c = 25 * 36 = 900`

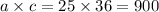
Factors of 900 are:

• 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 30, 36, 45, 50, 60, 75, 90, 100, 150, 180, 225, 300, 450, and 900.

Therefore, the factor pair that sums to 60 is 30 and 30.

Rewrite
`b` as the sum of these two numbers:

`25x^2 + 30x+30x + 36`

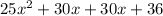
Factor the first two terms and the last two terms separately:

`5x(5x + 6)+6(5x+6)`

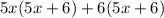
Factor out the common term (5x + 6):

`(5x+6)(5x+6)`

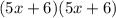
This can be written as:

`(5x+6)^2`