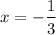Question

Division method to find the result when 9x³+24x²+16x+3 is 3x+1

Answer 1

Dividing 9x³+24x²+16x+3 by 3x+1 yields two quotients: x+2 and (3x+1)². These solutions correspond to roots at x=-2 and x=-1/3, respectively.

Let's find the result when 9x³+24x²+16x+3 is 3x+1 using division method.

We can solve the equation by moving all terms to the left side, distributing, subtracting the numbers, combining like terms, factoring the expression, creating separate equations, adding/subtracting to both sides, and dividing both sides of the equation by the same factor.

Steps to solve:

1. Move terms to the left side:

`$$9x^(3)+24x^(2)+16x+3-\left(3x+1\right)=0$$`

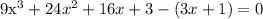
2. Distribute:

`$$9x^(3)+24x^(2)+16x+3-3x-1=0$$`

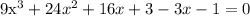
3. Subtract the numbers:

`$$9x^(3)+24x^(2)+16x+2-3x=0$$`

4. Combine like terms:

`$$9x^(3)+24x^(2)+13x+2=0$$`

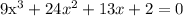
5. Factor the expression:

`$$(x+2)\left(9x^(2)+6x+1\right)=0$$`

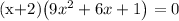
6. Factor the quadratic:

`$$(x+2)(3x+1)^(2)=0$$`

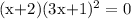
7. Create separate equations:

`$$x+2=0, \qquad 3x+1=0$$`

8. Solve the first equation:

`$$x+2=0$$`

`$$x=-2$$`

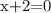
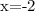
9. Solve the second equation:

`$3 x+1=0$`

`$3 x=-1$`

`$x=-(1)/(3)$`

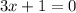
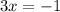
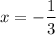
Answer:

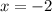`$x=-2 \quad$` or
`$\quad x=-(1)/(3)$`