Question

Finds of F across the curve C for the given vector field and curve using the Flux Form of Green's Theorem. In Exercises 38-43, compute the flux Ør. фF na 38. F(x, y) = (3x, 2y) across the circle given by x2 + y2 = 9 r 39. F(x, y) = (xy, x - y) across the boundary of the square -1

Answer 1

The flux across the circle
`\(x^2 + y^2 = 9\)` for the vector field
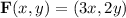`\(\mathbf{F}(x, y) = (3x, 2y)\)` is 0

The flux ф across a curve C for a given vector field
`\(F\)` using the Flux Form of Green's Theorem, you can use the following formula:

`\[\Phi = \iint_D \left((\partial Q)/(\partial x) - (\partial P)/(\partial y)\right) \,dA,\]`

where D is the region bounded by the curve C and P and Q are the components of the vector field
`\(F = \langle P, Q \rangle\).`

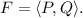
For
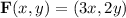`\(\mathbf{F}(x, y) = (3x, 2y)\)` and circle
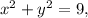`\(x^2 + y^2 = 9\),` we can parametrize the circle using polar coordinates:

`\[x = r \cos \theta,\]`

`\[y = r \sin \theta,\]`

where
`\(r = 3\)`

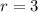
is the radius of the circle. The integral becomes:

`\[\Phi = \int_(0)^(2\pi) \int_(0)^(3) \left((\partial(2r \cos \theta))/(\partial r) - (\partial(3r \sin \theta))/(\partial \theta)\right) r \,dr \,d\theta.\]`

Let's compute this integral step by step:

`\[ \int_(0)^(2\pi) \int_(0)^(3) (2\cos \theta - 3r \cos \theta) \,dr \,d\theta\]`

`\[\int_(0)^(2\pi) \left[\left(r\Big|_(0)^(3) \cdot (2\cos \theta - 3r \cos \theta)\right) - \int_(0)^(3) -3\cos \theta \,dr\right] \,d\theta\]`

`\[\int_(0)^(2\pi) \left[3(2\cos \theta) + \int_(0)^(3) 3\cos \theta \,dr\right] \,d\theta\]`

`\[\int_(0)^(2\pi) \left[6\cos \theta + 3r\cos \theta\Big|_(0)^(3)\right] \,d\theta\]`

`\[ \int_(0)^(2\pi) \left[18\cos \theta + 9\cos \theta\right] \,d\theta\]`

`\[ \int_(0)^(2\pi) 27\cos \theta \,d\theta\]`

`\[ 27\int_(0)^(2\pi) \cos \theta \,d\theta\]`

`\[ 27\Big[\sin \theta\Big|_(0)^(2\pi)\Big]\]`

`\[27(0)\]`

`\[= 0.\]`

So, the flux across the circle
`\(x^2 + y^2 = 9\)` for the vector field
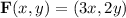`\(\mathbf{F}(x, y) = (3x, 2y)\)` is 0

For the second problem, with
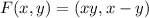`\(F(x, y) = (xy, x - y)\)` and the boundary of the square
`\([-1, 1]` times
`[-1, 1]\),`you need to parametrize the square and perform a similar integration as shown above. If you'd like assistance with that specific problem, let me know!