Question

In the sequence, 1, -2, -5, -8,... find the 26th term of the sequence

Answer 1

First, let's find the common difference of this sequence. The common difference is the amount that is added or subtracted each time in order to obtain the next term.

In this case, we're subtracting -3 each time, so, the common difference is -3.

We're given four terms: 1, -2, -5, -8; we're asked to find the 26th term.

In order to do it, we will apply a special formula, which is:

`\bf{a_n=a+(n-1)d}`

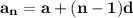
Where:

• 
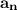  `\bf{a_n}` is the nth term;
• a is the first term in the sequence, which in this case is -1;
• n is the number of terms
• d is the common difference

The next step is to substitute the values into the formula.

The result is:

`\bf{a_n=1+(26-1)*(-3)}`

`\bf{a_n=1+25*(-3)}`

`\bf{a_n=1-75}`

`\bf{a_n=-74}`

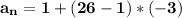
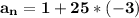
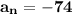
Therefore, the 26th term is -74.

Answer 2

a₂₆ = - 74

Explanation:

there is a common difference between consecutive terms in the sequence, that is

- 2 - 1 = 3

- 5 - (- 2) = - 5 + 2 = - 3

- 8 - (- 5) = - 8 + 5 = - 3

this means the sequence is arithmetic with nth term formula

`a_(n)` = a₁ + d(n - 1)

where a₁ is the first term , d the common difference and n the term number

here a₁ = 1 , d = - 3 and n = 26 , then

a₂₆ = 1 + (- 3 × 25) = 1 + (- 75) = 1 - 75 = - 74