Question

Find the sum of the sequence

42+43+44+45+ … +137


The sum is———-

Answer 1

the sum is 8592

Explanation:

the sequence has a common difference of 1 between consecutive terms.

this means the sequence is arithmetic with nth term formula

`a_(n)` = a₁ + d(n - 1)

where a₁ is the first term and d the common difference , n is the term number.

given that we know the first and last terms in the sequence then the sum to n terms is

`S_(n)` =
`(n)/(2)` ( first term + last term)

We require to find the number of terms in the sequence.

using the nth term formula with
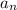`a_(n )` = 137 to find n

a₁ = 42 and d = 1

42 + 1(n - 1) = 137

42 + n - 1 = 137

41 + n = 137 ( subtract 41 from both sides )

n = 96

the sequence has 96 terms , then

sum =
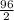`(96)/(2)` (42 + 137) = 48 × 179 = 8592

the sum is 8592