For a sequence xₙ ≥ 0 for all n ∈ N
a)
 , then
, then
 .
.
(b) If
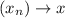 , then
, then
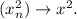
Let's prove both parts:
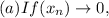
show that
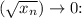
Given
 we want to show that
we want to show that
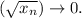
For any
 there exists N
there exists N
such that for all
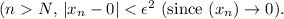
Now, observe that
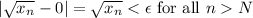
because
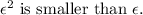 Therefore,
Therefore,
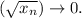
(b)
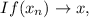 show that
show that
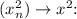
Given
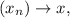
we want to show that
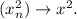 For any
For any

there exists
 such that for all
such that for all
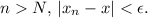
Now, consider
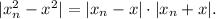 Since
Since
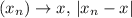
can be made arbitrarily small for
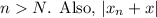 is bounded (it does not tend to infinity). Therefore,
is bounded (it does not tend to infinity). Therefore,
 trarily small for
trarily small for
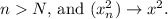
These proofs use the properties of limits and the fact that the square root and square functions are continuous.