Question

Please help me 50 pts!!

Answer 1

`\sf (9\pi)/(8) \textsf{sq units}`

Explanation:

The area of a sector is the portion of the circle enclosed by an arc and two radii.

The formula for the area of a sector is:

`\sf \textsf{ Area of sector }= (\pi)/(360^\circ) \pi r^2`

where:

• θ is the angle of the sector in degrees
• r is the radius of the circle
• π is the mathematical constant approximately equal to 3.141592654

In this case:

• Radius = 3 units
• 
  `\sf \textsf{Angle of sector }= (\pi)/(4)`

First convert radians to degrees.

we can convert radians to degrees by multiplying by:

`\sf ( 180^\circ)/(\pi)`

Now,

Substitute the value in above formula, we get;

`\begin{aligned} \textsf{Area of sector}&\sf = ((\pi)/(4)*(180^\circ)/(\pi))/(360^\circ)* \pi 3^2\\\\ &\sf = (1)/(8)\pi 3^2\\\\ &\sf = (9\pi)/(8) \textsf{sq units}\end{aligned}`

Answer 2

`(9\pi)/(8)\; \sf sq\;units`

Explanation:

To find the area of the sector, use the area of a sector formula (where the central angle is measured in radians).

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\frac12 r^2 \theta$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in radians.\\\end{minipage}}`

From inspection of the given diagram, the radius of the circle is 3 units, and the central angle of the sector is π/4 radians. Therefore:

• 
  `r = 3`

• 
  `\theta=(\pi)/(4)`

Substitute the values of r and θ into the formula, and solve for area (A):

`A=(1)/(2) \cdot 3^2 \cdot (\pi)/(4)`

`A=(1)/(2) \cdot 9 \cdot (\pi)/(4)`

`A=(9)/(2) \cdot (\pi)/(4)`

`A=(9\cdot \pi)/(2\cdot 4)`

`A=(9\pi)/(8)`

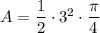
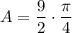
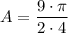
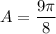
Therefore, the area of the sector is:

`\Large\boxed{\boxed{(9\pi)/(8)\; \sf sq\;units}}`