Answer: Infinite Solutions
Explanation:
In order to solve the inequality, isolate x.
Given inequality:
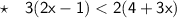
Use the distributive property:
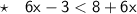
Add 3 to both sides
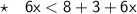
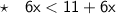
Subtract 6x from both sides

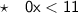
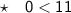
Since 0 is less than 11, this statement is true - and we know that any value of x will satisfy the inequality. Therefore, it has infinite solutions.