-------------------------------------------------------------------------------------------------------------
Answer:
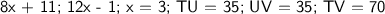
-------------------------------------------------------------------------------------------------------------
Given:
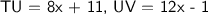
Find:
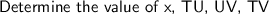
Solution: In order to determine the value of TU and UV, we need to first create an equation using the given information. We know that TU is equal to 8x + 11 and UV is equal to 12x - 1. Since we know that U is the midpoint, we know that TU is equal to UV. Therefore, the equation would have the following format: TU = UV
Now that we have the format, we can plug in the expressions and then simplify the equation.
Now, we can solve for x by adding 1 to both sides and then subtracting 8x from both sides.
We are now on the final step of solving for x. We just need to divide both sides by 4 to isolate the x variable and get the value of x.
Now that we have the value of x, we can plug it into the TU and UV expressions to determine what the length of the segments are.
Now that we now both sides of the segment, we can add them together to determine the length of the total segment.
Therefore, we know that the value of the variable x is equal to 3, the length of TU is 35, the length of UV is 35, the length of TV is 70.