-------------------------------------------------------------------------------------------------------------
Answer:
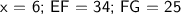
-------------------------------------------------------------------------------------------------------------
Given:

Find:

Solution: In order to determine the value of EF and FG, we need to first create an equation using the given information. We know that EF is equal to 8x - 14, FG is equal to 4x + 1, and EG is equal to 59. Therefore, the equation would have the following format: EF + FG = EG
Now that we have the format, we can plug in the expressions and then simplify the equation.
Now, combine like terms on the left side of the equation.
After combining like terms, we can solve for x by adding 13 to both sides and then dividing both sides by 12 to isolate the x variable.
Now that we have the value of x, we can plug it into the EF and FG expressions to determine what the length of the segments are.
Therefore, we know that the value of the variable x is equal to 6, the length of EF is 34 and the length of FG is 25.