Question

What is the distance between the two points at(-3,8) and(-3,-7)

Answer 1

Do you have someone pick up your line

Answer 2

`\boxed {\boxed {\sf 15}}`

Explanation:

Distance is calculated using this formula:

`d=\sqrt {(x_2-x_2)^2+(y_2-y_1)^2`

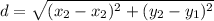
where (x₁, y₁) and (x₂, y₂) are the points. We are given (-3,8) and (-3,7). Therefore;

`x_1= -3 \\y_1= 8 \\x_2= -3 \\y_2= -7`

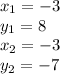
Substitute the values into the formula.

`d= \sqrt {(-3--3)^2+(-7-8)^2`

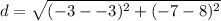
Solve inside the parentheses.

• -3 - - 3= -3+3= 0
• -7 - 8 = -15

`d= \sqrt {(0)^2+(-15)^2`

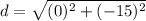
Solve the exponents.

• 0²=0*0= 0
• -15²= -15*-15=225

`d=\sqrt {0+225`

`d=\sqrt {225`
`d= \pm 15`

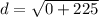
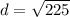
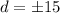
A negative number for distance doesn't make sense, so the distance must be 15.