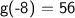Question

If g(x) = x^2 + x , what is g(-8)

Answer 1

Answer: 56

Explanation:

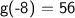
Given function:

g(x) = x^2 + x

We know that the value of x is -8. So I plug it into the function.

g(-8) = (-8)^2 + (-8)

g(-8) = 64 - 8

g(-8) = 56

Therefore, g(-8) = 56.

Answer 2

-------------------------------------------------------------------------------------------------------------

Answer:
`\textsf{g(-8) = 56}`

-------------------------------------------------------------------------------------------------------------

Given:
`\textsf{g(x) = x}^2\textsf{ + x}`

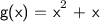
Find:
`\textsf{The solution of g(-8)}`

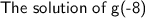
Solution: In order to start working toward the solution, we need to initially set the value of x in the equation to -8.

`\textsf{g(x) = x}^2\textsf{ + x}`

`\textsf{g(-8) = (-8)}^2\textsf{ + (-8)}`

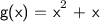
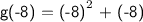
Now, that we have replaced the x variable with -8, we can now simplify the values and combine them to get the final solution. The first number,
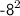`\textsf{-8}^2` is the same as
`\textsf{(-8) * (-8)}` which turns out to be 64. We can now subtract 8 from 64 to get our final answer of 56.

Therefore, the final answer is
`\textsf{g(-8) = 56}`