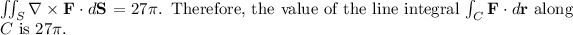Question

Evaluate ∫ C

​
(−z i
+y j
​
+3x k
)⋅d r
, where C is a circle of radius 3 , parallel to the xz-plane and around the positive y-axis with counterclockwise orientation when viewed from a point on the y-axis far from the origin. ∫ C
​
(−z i
+y j
​
+3x k
)⋅d r
=

Answer 1

The value of
`\( \int_C (-z \mathbf{i} + y \mathbf{j} + 3x \mathbf{k}) \cdot d\mathbf{r} \) along the described circle \( C \) is \( 27\pi \).`

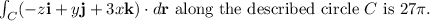
Step-by-step explanation:

Given the vector field
`\( \mathbf{F} = (-z \mathbf{i} + y \mathbf{j} + 3x \mathbf{k}) \) and the closed curve \( C \) described as a circle of radius 3 parallel to the \( xz \)-`plane around the positive y-axis in a counterclockwise orientation, we want to compute the line integral
`\( \int_C \mathbf{F} \cdot d\mathbf{r} \)`along this curve.

To evaluate this line integral, we can utilize Stokes' theorem. Since the curve \( C \) is a circle lying in the \( xz \)-plane with a radius of 3 around the y-axis, the curve is a planar loop and lies in a plane normal to the \( y \)-axis.

Stokes' theorem states that the line integral of a vector field \( \mathbf{F} \) over a closed curve \( C \) is equal to the flux of the curl of \( \mathbf{F} \) through the surface enclosed by \( C \). In this case, the surface enclosed by the curve \( C \) is a disk in the \( xz \)-plane with the same radius as the circle.

The vector field
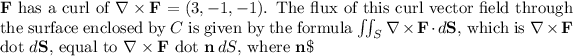`\( \mathbf{F} \) has a curl of \( \\abla * \mathbf{F} = (3, -1, -1) \). The flux of this curl vector field through the surface enclosed by \( C \) is given by the formula \( \iint_S \\abla * \mathbf{F} \cdot d\mathbf{S} \), which is \( \\abla * \mathbf{F} \) dot \( d\mathbf{S} \), equal to \( \\abla * \mathbf{F} \) dot \( \mathbf{n} \, dS \), where \( \mathbf{n} \`) is the outward unit normal vector to the surface.

Applying this knowledge, the surface integral computes to
`\( \iint_S \\abla * \mathbf{F} \cdot d\mathbf{S} = 27\pi \). Therefore, the value of the line integral \( \int_C \mathbf{F} \cdot d\mathbf{r} \) along \( C \) is \( 27\pi \).`