Question

The top of a ladder slides down a vertical wall at a rate of 0.375 m/s. At the moment when the bottom of the ladder 6 m from the wall is slides away from the water rate of 0.5 m/s. How long is the ladder?

Answer 1

The length of the ladder is 8 m.

To solve this problem, you can use the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other sides a and b:

`\[c^2 = a^2 + b^2\]`

In this case, the ladder is the hypotenuse, the wall is one side (let it be a), and the distance the bottom of the ladder moves away from the wall is the other side (let it be b). The ladder itself is c.

Given that the bottom of the ladder is moving away from the wall, we can use the rates of change to relate a, b, and c. The relationship is given by the equation:

`\[c (dc)/(dt) = a (da)/(dt) + b (db)/(dt)\]`

Here, c is the length of the ladder, a is the distance from the wall, b is the distance the bottom of the ladder is moving away from the wall, and t is time.

Given values:

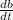`\[(db)/(dt)` = 0.5 m/s (rate at which the bottom is sliding away)

b = 6 m (distance from the wall)

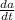`\[(da)/(dt)` = 0 m/s (the distance from the wall is not changing)

Substituting the values:

c x 0.375 = 6 x 0 + 0.5 x 6

0.375 c = 3

c =
`(3)/(0.375)`

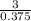
c = 8 m

So, the length of the ladder is 8 meters.