Question

Find the equation for the circle with a diameter whose endpoints are (5,15) and (1, - 11).

Answer 1

`(x-3)^2+(y-2)^2=173`

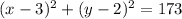
Explanation:

To find the equation of a circle with a diameter whose endpoints are (5, 15) and (1, - 11), we first need to find its center and radius.

The center of a circle is the midpoint of the endpoints of its diameter.

To find the center, we can use the midpoint formula.

`\boxed{\begin{array}{l}\underline{\sf Midpoint \;formula}\\\\M(x,y) =\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)\\\\\textsf{where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.}\\\end{array}}`

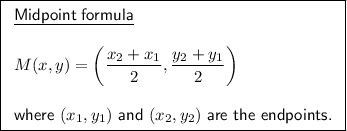
Substitute the endpoints (5, 15) and (1, - 11) into the midpoint formula:

`C(x,y) =\left((1+5)/(2),(-11+15)/(2)\right)`

`C(x,y) =\left((6)/(2),(4)/(2)\right)`

`C(x,y) =\left(3,2\right)`

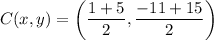
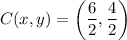
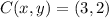
Therefore, the center of the circle is (3, 2).

The radius is half the diameter, so the distance between the center and one of the endpoints of the diameter. To find the radius, we can use the distance formula.

`\boxed{\begin{array}{l}\underline{\sf Distance \;Formula}\\\\d=√((x_2-x_1)^2+(y_2-y_1)^2)\\\\\textsf{where:}\\ \phantom{ww}\bullet\;\;d\;\textsf{is the distance between two points.} \\\phantom{ww}\bullet\;\;\textsf{$(x_1,y_1)$ and $(x_2,y_2)$ are the two points.}\\\\\end{array}}`

Substitute the center (3, 2) and one of the endpoints (5, 15) into the distance formula to find the radius of the circle:

`r=√((5-3)^2+(15-2)^2)`

`r=√((2)^2+(13)^2)`

`r=√((4+169))`

`r=√(173)`

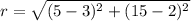
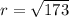
The standard equation of a circle with center (h, k) and radius r is:

`(x-h)^2+(y-k)^2=r^2`

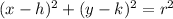
Substitute the found center (3, 2) and radius √(173) into the equation:

`(x-3)^2+(y-2)^2=(√(173))^2`

`(x-3)^2+(y-2)^2=173`

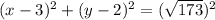
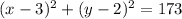
Therefore, the equation for the circle with a diameter whose endpoints are (5, 15) and (1, -11) is:

`\Large\boxed{\boxed{(x-3)^2+(y-2)^2=173}}`