Question

Model for cost:

C(x)=0.003x^2-7.8x+15000
x=# of items produced per week
how many items should be produced per week to minimize cost?

Answer 1

To find the number of items that should be produced per week to minimize cost, you can use calculus to find the minimum point of the cost function. The cost function is given as:

C(x) = 0.003x^2 - 7.8x + 15000

To minimize cost, you need to find the value of x (the number of items produced per week) that makes the derivative of C(x) equal to zero, and then check if this point is a minimum or maximum by examining the second derivative.

First, find the derivative of C(x):

C'(x) = 0.006x - 7.8

Now, set this derivative equal to zero and solve for x:

0.006x - 7.8 = 0

0.006x = 7.8

x = 7.8 / 0.006

x ≈ 1300

So, approximately 1300 items should be produced per week to minimize cost. To confirm that this is indeed a minimum, you can check the second derivative of the cost function. If the second derivative is positive at x ≈ 1300, it confirms that it's a minimum point.

Answer 2

1,300 items

Explanation:

Given cost function:

`C(x)=0.003x^2-7.8x+15000`

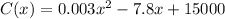
where x is the number of items produced per week.

The given cost function C(x) is a quadratic equation with a positive leading coefficient, which means its graph is a parabola that opens upwards.

In such cases, the vertex of the parabola represents the minimum point of the function. Therefore, to minimize the cost, we need to find the vertex of the function. The x-coordinate of the vertex is the number of items that should be produced per week to minimize cost.

In a quadratic equation of the form y = ax² + bx + c, the x-coordinate of the vertex can be found using the formula x = -b/2a​.

For the given function C(x):

• a = 0.003
• b = -7.8
• c = 15000

Substitute the values of a and b into the formula to find the x-coordinate of the vertex:

`x=(-(-7.8))/(2\cdot 0.003)=(7.8)/(0.006)=1300`

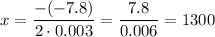
Therefore, 1,300 items should be produced per week to minimize cost.