Question

Solve this, it has two answers please help me 3|x+6|-7=20

Answer 1

• x = 3 and -15

Task :

• To evaluate 3|x+6|-7=20

Solution :

• 
  `3|x+6|-7=20`
• 
  `3|x+6|-7 + 7=20 + 7`
• 
  `3|x+6|=27`
• 
  `(3|x+6|)/(3) = (27)/(3) \\`
• 
  `|x+6|=9`
• 
  `|x+6| =( x + 6) \: and \: - (x + 6)`
• 
  `x + 6 = 9`
• 
  `x = 9 - 6`
• 
  `x = 3`
• 
  `- (x + 6) = 9`
• 
  `- x - 6 = 9`
• 
  `- x = 9 + 6`
• 
  `- x = 15`
• 
  `x = - 15`

Hence, x = 3 and -15.

Answer 2

x = 3 and x = -15

Explanation:

In order to solve the equation 3|x + 6| - 7 = 20, we need to isolate the absolute value expression and solve for x.

`\sf 3|x + 6| - 7 = 20`

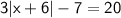
Add 7 to both sides of the equation:

`\sf 3|x + 6| - 7 + 7 = 20 + 7`

`\sf 3|x + 6| = 27`

Divide both sides by 3 to isolate the absolute value expression:

`\sf ((3|x + 6|))/(3) = (27)/(3)`

`\sf |x + 6| = 9`

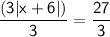
We have an absolute value equation. To solve for x, we'll consider two cases:

• when the expression inside the absolute value is positive and
• when it's negative.

Case 1:

x + 6 is positive (x + 6 > 0)

In this case, the absolute value bars can be removed, and the equation becomes:

`\sf x + 6 = 9`

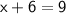
Subtract 6 from both sides:

`\sf x = 9 - 6`

`\sf x = 3`

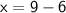
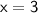
Case 2:

x + 6 is negative (x + 6 < 0)

In this case, the absolute value bars can be removed, but we need to negate the expression inside:

`\sf -(x + 6) = 9`

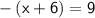
Multiply both sides by -1 to make the expression positive:

`\sf x + 6 = -9`

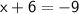
Subtract 6 from both sides:

`\sf x = -9 - 6`

`\sf x = -15`

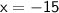
So, the equation has two solutions:

x = 3 and x = -15.