Question

Find area of a triangle 17 sides 15 height

Answer 1

120 square inches.

Explanation:

Area of triangle is calculated by using formula:

`\sf Area =(1)/(2) base * height`

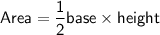
In this case:

• Height = 15 in
• Hypotenuse= 17 in

Since over here there is not a base.

We can find a base by using the Pythagoras theorem:

Pythagoras' theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

In this case:

Using the Pythagorean theorem:

`\sf Hypotenuse^2 = Base^2 + Height^2`

`\sf 17^2 = b^2 + 15^2`

`\sf 289 = b^2 + 225`

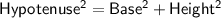
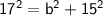
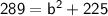
Now, solve for "b":

`\sf b^2 = 289 - 225`

`\sf b^2 = 64`

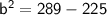
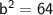
Taking Square root on both sides:

`\sf b = √(64)`

`\sf b = 8`

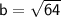
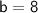
Since there are 2 congruent triangles, the new combined base is 2 × 8 = 16 in

Now,

Substitute the value of new combined base and height in the formula of area; we get

`\begin{aligned} \textsf{ Area }&\sf = (1)/(2)* 16* 15 \\\\&\sf = 8* 15 \\\\ &\sf = 120 in^2 \end{aligned}`

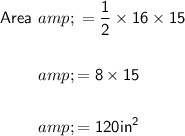
So, the area of the triangle is 120 square inches.