Answer:
6th term = 30
Explanation:
5, 10, 15, 20, ...
The given sequence is an arithmetic sequence because each term is obtained by adding a fixed value to the previous term.
In this case, the common difference (the value added to each term to get the next term) is 5.
To describe this sequence using an expression, we can use the formula for an arithmetic sequence:
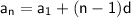
Where:
- an is the nth term in the sequence.
- a1 is the first term.
- n is the position of the term in the sequence.
- d is the common difference.
In this sequence:
- a1 is the first term, which is 5.
- The common difference, d, is 5.
So, the expression for the sequence by the substitution of value is:
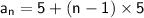
Now, to find the 6th term (where n = 6), substitute n = 6 into the expression:
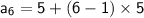
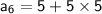
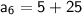
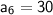
So, the 6th term of the sequence is 30.