Question

Determine the slope of the line that passes through the given points.

(-3,5), (10,5)
75
0 2
Undefined
10-2
0
상

Answer 1

Zero

Given :

• Two points (-3,5) ,(10,5)

To find :

• Slope of the line that passes through these points

Solution :

We know that,

• Slope of a line = [y2 - y1]/[x2 - x1]

where,

• x1 & y1 = coordinates of first point
• x2 & y2 = coordinates of second point

ATQ,

• x1 = -3
• y1 =5
• x2 = 10
• y2 = 5

and

• Slope of the line = [5 - 5]/10 + 3]
• Slope of the line = 0/13
• Slope of the line = 0

Therefore,the slope of the line would be zero.

Answer 2

Slope = 0

Explanation:

Given:

Two points:(-3, 5) and (10, 5)

To find:

Slope:

Solution:

We can use the following formula for the slope of a line:

`\sf \textsf{Slope} (m) = \frac{\text{Change in } y}{\textsf{Change in } x}`

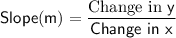
In this case, we have two points: (-3, 5) and (10, 5).

The change in y (the vertical change) is the difference in the y-coordinates of the two points:

`\sf \Delta y = 5 - 5 = 0`

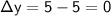
The change in x (the horizontal change) is the difference in the x-coordinates of the two points:

`\sf \Delta x = 10 - (-3) = 10 + 3 = 13`

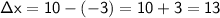
We can calculate the slope using the formula by substituting value:

`\sf m = (\Delta y)/(\Delta x) = (0)/(13) = 0`

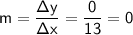
So, the slope of the line that passes through the points (-3, 5) and (10, 5) is 0.