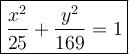Question

Instructions: Use the information provided to write the standard form equation of each ellipse. Vertices: (0, -13), (0, 13) Foci: (0, -12), (0, 12)

Hint:(The answer is not x^2/169+y^2/25=1, and a way to start off the standard equation form would be x^2/?+y^2/?=1)​

Answer 1

`(x^2)/(25)+(y^2)/(169)=1`

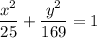
Explanation:

Given:

• Vertices (0, ±13)
• Foci (0, ±12)

As the x-values of the vertices and foci are the same, the major axis of the ellipse is vertical, and therefore the ellipse is vertical. The center (h, k) of the ellipse is (0, 0).

`\boxed{\begin{minipage}{8 cm}\underline{General equation of a vertical ellipse}\\\\$((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center.\\\phantom{ww}$\bullet$ $(h,k\pm a)$ are the vertices.\\\phantom{ww}$\bullet$ $(h,k\pm c)$ are the foci where $c^2=a^2-b^2$.\\\end{minipage}}`

Equate the vertices formula with the actual vertices and solve for a:

`\begin{aligned}(h, k \pm a) & = (0, \pm 13)\\(0, 0 \pm a) & = (0, \pm 13)\\(0, \pm) & = (0, \pm 13)\\a& =13\end{aligned}`

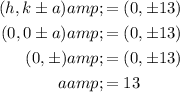
Equate the foci formula with the actual foci and solve for c:

`\begin{aligned}(h, k \pm c) & = (0, \pm 12)\\(0, 0 \pm c) & = (0, \pm 12)\\(0, \pm c) & = (0, \pm 12)\\c& =12\end{aligned}`

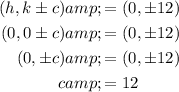
To find b, substitute the found values of a and c into c² = a² - b²:

`\begin{aligned} c^2&=a^2-b^2\\12^2&=13^2-b^2\\b^2&=13^2-12^2\\b^2&=169-144\\b^2&=25\\b&=5\end{aligned}`

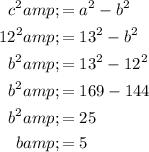
To create an equation of the ellipse with the given properties, substitute the values of h, k, a and b into the general equation of an ellipse:

`\begin{aligned}((x-0)^2)/(5^2)+((y-0)^2)/(13^2)&=1\\\\(x^2)/(25)+(y^2)/(169)&=1\end{aligned}`

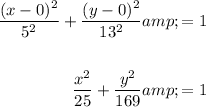
Therefore, the standard form equation of the ellipse with vertices (0, ±13) and foci (0, ±12) is:

`\large\boxed{(x^2)/(25)+(y^2)/(169)=1}`