Question

If
`(5)/(x + 2) = (5 - x)/(x - 2) + 1`, then x = _____?


`\\`
A. 2
B. -8
C. 8
D. -2​

Answer 1

To solve the given equation, we can start by simplifying both sides of the equation.

I hope this helps

Answer 2

c. 8

Explanation:

`\sf (5)/(x + 2) = (5 - x)/(x - 2) + 1`

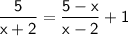
Taking L.C. M. on the right side.

`\sf (5)/(x + 2) = (5 - x +(x-2))/(x - 2)`

Simplify like terms on the right-hand side

`\sf (5)/(x + 2) = (5 - x +x-2)/(x - 2)`

`\sf (5)/(x + 2) = (3)/(x - 2)`

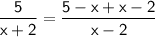
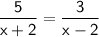
Now, doing criss-cross multiplication:

`\sf 5(x-2)=3(x+2)`

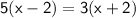
Open the parenthesis

`\sf 5x - 10 = 3x + 6`

Subtracting both sides by 3x

`\sf 5x-10-3x = 3x +6 -3x`

Simplify like terms

`\sf 2x - 10 = 6`

Add 10 on both sides:

`\sf 2x - 10+10 = 6+10`

`\sf 2x = 16`

Divide both sides by 2:

`\sf (2x)/(2)=(16)/(2)`

`\sf x = 8`

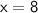
Therefore, the answer is c. 8