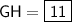Question

If G is the midpoint of FH, FG = 2x - 3, what is GH?

Answer 1

`\sf x = \boxed{\sf 7}`

`\sf GH =\boxed{ \sf 11 }`

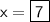
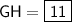
Explanation:

Given:

`\sf FG = 2x -3`

`\sf FH = 22`

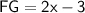
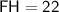
If point G is the midpoint of line segment FH, then it means that FG is equal in length to GH.

In other words:

`\sf FG = GH`

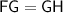
And we have,

`\sf FH = FG + GH`

`\sf FH = FG + FG`

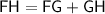
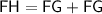
Since FG = GH

`\sf FH = 2FG`

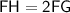
Substitute the value

`\sf 22 = 2(2x-3)`

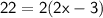
Open the bracket

`\sf 22 = 4x - 6`

Add 6 on both sides

`\sf 22 +6 = 4x`

`\sf 28 = 4x`

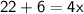
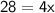
Divide both sides by 4.

`\sf (28)/(4) = x`

`\sf x = \boxed{\sf 7}`

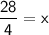
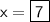
Now,

`\sf GH = FG = 2* 7 - 3 = 14-3 = 11`

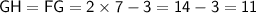
So,

`\sf GH =\boxed{\sf 11 }`