Question

Reagen ran 3/4 mile in 1/4 hour. Write Ann equation for the distance in miles y that she ran in x if she ran at a constant rate

Answer 1

y = 3x

Explanation:

`(y)/(x) =((3/4))/((1/4))`

`(y)/(x) =(3)/(1)`

`y=3x`

Answer 2

`\boxed{\sf y = 3x }`

Explanation:

`\sf textsf{ Reagen ran } \sf (3)/(4)\textsf{ mile in }\sf (1)/(4) hour.`

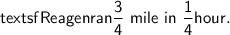
In order to write an equation for the distance in miles (y) that she ran in x hours, assuming she ran at a constant rate, we can use the formula for distance:

`\sf Distance (y) = Rate (R) * Time (x)`

In this case,

`\sf textsf{ Reagen ran } \sf (3)/(4)\textsf{ mile in }\sf (1)/(4) hour.`

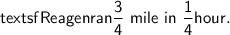
We need to find her rate:

`\sf Rate (R) = (Distance )/( Time )`

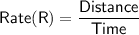
Substitute the value

`\begin{aligned} \textsf{Rate(R) } &\sf =( (3)/(4) )/( (1)/(4) ) \\\\&\sf = (3)/(4)* (4)/(1) \\\\ &\sf = 3 mile/hour \end{aligned}`

Now that we have her rate (R), we can write the equation for the distance she ran in x hours:

`\sf Distance (y) = Rate (R) * Time (x)`

Substitute the value:

`\sf y = 3x`

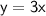
So, the equation for the distance in miles (y) that Reagen ran in x hours at a constant rate is:

`\boxed{\sf y = 3x }`