Question

Use long or synthetic division to find the following quotients
(x^3+2x^2!22x-45)÷(x+5) ​

Answer 1

`\boxed{\textsf{ The quotient is $\sf x^2-3x-7$ and the remainder is (-10).}}`

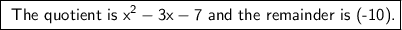
Explanation:

Here we will be using long division method to find the quotient . Here we need to divide (x³+2x²-22x-45) and (x+5) . So lets divide .

x+5) x³+2x²-22x-45 ( x² -3x -7

x³ + 5x²

- -

______________

- 3x²-22x -45

-3x² -15x

+ +

______________

-7x -45

-7x -35

______________

-10

Quotient = x² -3x -7

Remainder = (-10)

★Hence the quotient is x² -3x -7 and the remainder is (-10) .