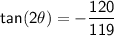Question

HELPPPPP PLEASEEEEEEEE. 25pts!!!!

Answer 1

sin A = 12/13, so cos A = 5/13 and

tan A = 12/5

tan 2A = 2(12/5)/(1 - (12/5)²)

= (24/5)/(1 - 144/25)

= (24/5)/(-119/25)

= (24/5)(-25/119)

= -120/119

Answer 2

`\sf tan(2\theta) = - (120)/(119)`

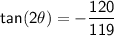
Explanation:

Since θ is in the first quadrant, sinθ and cosθ are both positive.

`\sf sin \theta = (12)/(13)`

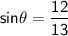
We know the following identity to find tan 2θ:

`\sf tan(2\theta) = (2tan(\theta))/(1 - tan^2(\theta))`

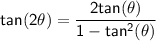
First, let's find tan 2θ using the information given:

`\sf tan(\theta) = (sin(\theta))/(cos(\theta))`

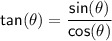
We already know that :

`\sf sin(\theta) = (12)/(13)`

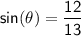
To find, cosθ we can use the Pythagorean identity:

`\sf \cos^2(\theta) = 1 - \sin^2(\theta)`

`\sf \cos^2(\theta)= 1 - \left((12)/(13)\right)^2`

`\sf \cos^2(\theta) =1 - (144)/(169)`

`\sf \cos^2(\theta)= (169 - 144)/(169)`

`\sf \cos(\theta)= \sqrt{(25)/(169)}`

`\sf cos(\theta)= (5)/(13)`

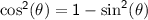
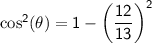
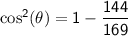
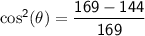
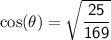
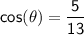
Now, we can find tan θ.

`\begin{aligned}\sf tan(\theta) &\sf= (sin(\theta))/(cos(\theta)) \\\\&\sf = ((12)/(13))/((5)/(13)) \\\\&\sf = (12)/(5) \end{aligned}`

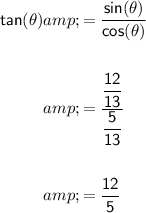
Now, we can use tan θ to find tan 2θ using the double-angle formula:

`\begin{aligned}\sf tan(2\theta) &\sf = (\tan(\theta))/(1 - tan^2(\theta)) \\\\&\sf= (2\left((12)/(5)\right))/(1 - \left((12)/(5)\right)^2) \\\\&\sf = ((24)/(5))/(1 - (144)/(25)) \\\\&\sf = ((24)/(5))/(1 - (144)/(25)) \\\\&\sf = ((24)/(5))/((25)/(25) - (144)/(25)) \\\\ &\sf = ((24)/(5))/((-119)/(25)) \\\\&\sf = (24)/(5) \cdot (-25)/(119)\\\\&\sf = -(120)/(119) \end{aligned}`

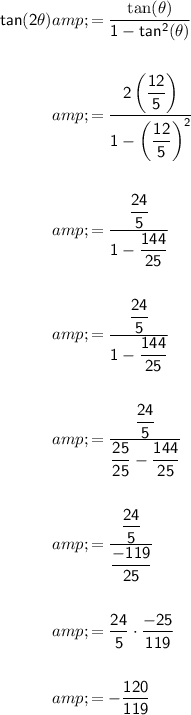
So,

`\sf tan(2\theta) = - (120)/(119)`