Question

C is the midpoint of BE. If BC = t+1 and CE = 15-t, What is BE?

Answer 1

Hello!

Answer:

`\Large \boxed{\sf BE = 16}`

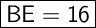
Explanation:

→ We want to calculate BE.

→ We know that:

- C is the midpoint of BE

- BC = t + 1

- CE = 15 - t

→ So we know that BC = CE since C is the midpoint of BE.

→ So we have this equation:

`\sf BC = CE`

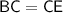
→ Let's replace BC by t + 1 and CE by 15 - t:

`\sf t+1 = 15-t`

→ Let's solve this equation:

◼ Subtract 1 from both sides:

`\sf t+1-1 = 15-t-1`

◼ Simplify both sides:

`\sf t= 14-t`

◼ Add t to both sides:

`\sf t+t= 14-t+t`

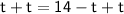
◼ Simplify both sides:

`\sf2t= 14`

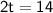
◼ Divide both sides by 2:

`\sf (2t)/(2) = (14)/(2)`

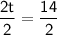
◼ Simplify both sides:

`\boxed{\sf t = 7}`

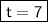
→ Now, we know that t = 7.

→ We also know that BE = BC + CE.

→ So we have this equation:

`\sf BE = BC + CE`

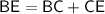
→ Let's replace BC by t + 1 and CE by 15 - t:

`\sf BE = t+1+15-t`

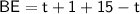
→ Let's replace t by 7 to find BE:

`\sf BE = 7+1+15-7`

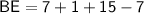
→ Let's simplify the right side to find BE:

`\boxed{\sf BE = 16}`

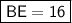
Conclusion:

BE is equal to 16.