Question

A man invest $2400 some at 9.5% annual interest the balance at 7% annual interest if he receives $208 in interest yearly how much did he invested each rate

Answer 1

The man invested $1600 at 9.5% interest and $800 at 7% interest.

Explanation:

Let's denote the amount invested at 9.5% as x dollars and the amount invested at 7% as 2400 - x dollars (since the total investment is $2400).

We are given that the total interest received yearly is $208.

We have:

The formula to calculate interest is:

`\sf Interest =( Principal * Rate * Time)/(100)`

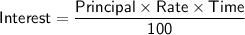
First, we'll calculate the interest earned from the amount invested at 9.5% annually.

`\begin{aligned} \textsf{Interest from 9.5\%} &\sf =( x * 9.5 * 1 )/(100) \\\\=&\sf 0.095x \end{aligned}`

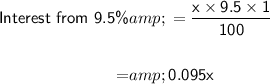
Next, we'll calculate the interest earned from the amount invested at 7% annually.

`\begin{aligned} \sf \textsf{Interest from 7\% } &\sf = ((2400 - x) * 7 * 1 )/(100) \\ \\&\sf = (2400-x)* 0.07\\\\&\sf = 2400* 0.07 - x* 0.07 \\ \\&\sf = 168 - 0.07x \end{aligned}`

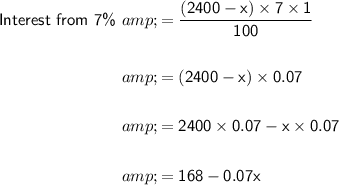
According to the problem, the total interest received yearly is $208.

So, we can set up the equation:

`\textsf{ Interest from 9.5\% + Interest from 7\% = Total Interest}`

`\sf 0.095x + 168 - 0.07x = 208`

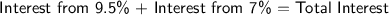
Combine like terms:

`\sf 0.095x - 0.07x + 168 = 208`

`\sf 0.025x + 168 = 208`

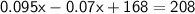
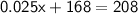
Subtract 168 from both sides:

`\sf 0.025x = 208 - 168`

`\sf 0.025x = 40`

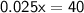
Divide by 0.025 to solve for x:

`\sf x =( 40 )/(0.025)`

`\sf x = 1600`

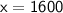
So, the man invested $1600 at 9.5% interest, and the remaining amount, which is $2400 - $1600 = $800, was invested at 7% interest.