Question

2.5x^4+3x^3-2.6x^2-5.1x-5.6 On the closed interval (-0.5, 1.2], determine the absolute minimum output value of find the absolute maximum output value of f. Label your answers appropriately.

Answer 1

Minimum : f(0.2) = -6.696

Maximum : f(-0.8) = -3.696

Given :

• f(x) = 2.5x^4+3x^3-2.6x^2-5.1x-5.6

To find :

• The absolute minimum and maximum output value of f on the closed interval of (-0.5, 1.2)

Solution :

• f(x) = 2.5x^4+3x^3-2.6x^2-5.1x-5.6
• f(x)' = 10x^3 + 9x^2 -5.2x -5.1
• f(x)'' = 30x² + 18x - 5.2

using quadratic formula to find the roots :

• x = [-b ± √(b^2 - 4ac)]/2a

Where,

• a = 30
• b = 18
• c = -5.2

Hence,

• x = [-18 ± √(18^2 -4*30*-5.2)]/2*30
• x = [-18 ± √(948)]/60
• x = [-18 ± 2√(237)]/60
• x_1 = [-18 + 2√(237)]/60
• x_1 = 0.2
• x_2 = [-18 - 2√(237)]/60
• x_2 = -0.8

Therefore, x = 0.2 or -0.8

ATQ,

• Interval = (-0.5, 1.2)

Thereby,Calculating f(x) at -0.8,-0.5,0.2 & 1.2

• f(-0.8)= -3.696
• f(-0.5) = -3.919
• f(0.2) = -6.696
• f(1.2) = -5.096

Hence,the absolute maximum output value is -3.696 at x = -0.8 and minimum output value is -6.696 at x = 0.2

Answer 2

Absolute minimum output value = -8.832 (3 d.p.)

Absolute maximum output value = -3.919 (3 d.p.)

Explanation:

Given function:

`f(x)=2.5x^4+3x^3-2.6x^2-5.1x-5.6`

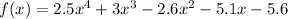
The absolute minimum output value of a function on a specific interval is the smallest value that the function takes within that interval. In other words, it's the lowest point that the function reaches, considering all the values it outputs on that interval. It can occur at a critical point, an endpoint of the interval, or even at a point where the function is not differentiable.

The absolute maximum output value of a function on a specific interval is the largest value that the function takes within that interval. In other words, it's the highest point that the function reaches, considering all the values it outputs on that interval. Similar to the absolute minimum, the absolute maximum can occur at critical points, endpoints of the interval, or points where the function is not differentiable.

Begin by evaluating the endpoints of the interval [-0.5, 1.2]:

`\begin{aligned}f(-0.5)&=2.5(-0.5)^4+3(-0.5)^3-2.6(-0.5)^2-5.1(-0.5)-5.6\\&=0.15625-0.375-0.65+2.55-5.6\\&=-3.91875\end{aligned}`

`\begin{aligned}f(1.2)&=2.5(1.2)^4+3(1.2)^3-2.6(1.2)^2-5.1(1.2)-5.6\\&=5.184+5.184-3.744-6.12-5.6\\&=-5.096\end{aligned}`

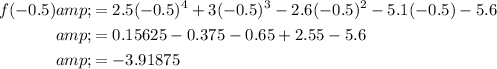
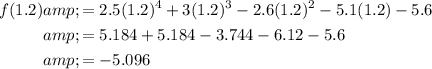
The critical points of a function are the points where the derivative of the function is either zero or undefined.

Differentiate the given function:

`f'(x)=4\cdot2.5x^(4-1)+3\cdot3x^(3-1)-2\cdot2.6x^(2-1)-5.1-0`

`f'(x)=10x^3+9x^2-5.2x-5.1`

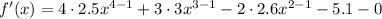
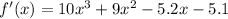
Set f'(x) equal to zero and solve for x using a calculator:

`\begin{aligned}f'(x)&=0\\10x^3+9x^2-5.2x-5.1&=0\\x&=0.738668106...\end{aligned}`

Substitute the found x-coordinate of the critical point into the function to find its y-coordinate:

`f(0.738668106...)=-8.8324453...`

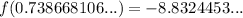
Therefore, the critical point of function f(x) is (0.739, -8.832) (3 d.p.).

In conclusion, the endpoints and critical point of the function on the closed interval [-0.5, 1.2] are:

• (-0.5, -3.91875)
• (1.2, -5.096)
• (0.739, -8.832)

Therefore, the absolute minimum output value is -8.832 (3 d.p.) and the absolute maximum output value is -3.919 (3 d.p.).