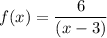Question

What is the vertical asymptote of the function?x = –5x = –3x = 3x = 5

Answer 1

The vertical asymptote of the function is x = 0.

Step-by-step explanation:

A vertical asymptote of a function is a vertical line that the graph of the function approaches as x approaches a particular value. In this case, the given values of x are -5, -3, 3, and 5. To determine the vertical asymptotes, we need to find the values of x where the function is undefined. Since the function is undefined when the denominator is zero, we set the denominator equal to zero and solve for x:

-5x = 0 --> x = 0

-3x = 0 --> x = 0

3x = 0 --> x = 0

5x = 0 --> x = 0

Therefore, the vertical asymptote of the function is x = 0.

Answer 2

The vertical asymptote for the function
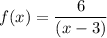`f(x) = (6 )/((x - 3))` is x = 3.

What is the vertical asymptote of a function.

The vertical asymptote of a function is a vertical line that the function approaches on the graph but does not touch it when the input variable (x) reaches a specific value.

For a rational function
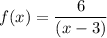`f(x) = (6 )/((x - 3))`. The vertical asymptote takes place when the denominator is equal to zero. i.e.

x - 3 = 0

x = 3

This means that the graph will approach the vertical line as x gets near to 3.

Therefore, we can conclude that the vertical asymptote for the function
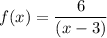`f(x) = (6 )/((x - 3))` is x = 3.

The complete question.

What is the vertical asymptote of the function.
`f(x) = (6 )/((x - 3))`