Question

If JK = 8, KL = x + 4, and JL = 3x, what is JL?

Answer 1

JL = 18

Explanation:

Given:

`\sf JK = 8`

`\sf KL = x + 4`

`\sf JL = 3x`

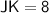
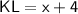
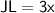
We know that in a straight line, the sum of the lengths of the segments is equal to the total length.

So, we can set up an equation:

`\sf JK + KL = JL`

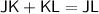
Substitute the given values:

`\sf 8 + (x + 4) = 3x`

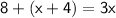
Now, let's solve for x:

Combine like terms on the left side:

`\sf 8 + x + 4 = 3x`

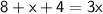
Combine constants:

`\sf 12 + x = 3x`

Subtract x from both sides to isolate the x terms:

12 = 2x

Divide both sides by 2 to solve for x:

`\sf x =( 12 )/(2)`

x = 6

Now that we have found the value of x, we can find JL using the equation given for JL:

`\sf JL = 3x`

`\sf JL = 3 * 6`

`\sf JL = 18`

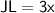
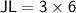
So, JL is equal to 18.