Question

Parallel to the line y = -3x; containing the point (- 1, 2)

Answer 1

y = -3x - 1

Explanation:

Parallel lines have the same slope

If you want to find the equation parallel to y = -3x and crosses the point (-1,2), meaning they have the same slope of -3

the slope form of the equation is y = mx + b

substitute the slope and a pair of coordinate to find the y-intercept

y = mx + b

2 = -1(-3) + b

2 = 3 + b

2 - 3 = b

b = -1

Therefore the equation parallel to y = -3x and crosses the point (-1,2) is

y = -3x - 1

Answer 2

Answer: y = -3x - 1

Explanation:

In order to write the equation of the line, we will first identify the givens.

givens:

• the line is parallel to y = -3x
• the line contains the point (-1,2)

main idea:

• parallel lines have the same slope

So, we conclude that the new line has the same slope as y = -3x - a slope of -3.

Now, all we need to do is plug in the values into our point-slope formula:

`\bigstar\quad\sf{y-y_1=m(x-x_1)}`

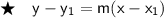
where:

• 
  `m=slope`
• 
  `(x_1,y_1) \ is \ a \ point`

Insert these values into the formula:

`\twoheadrightarrow\quad\sf{y-2=-3(x-(-1)}`

`\twoheadrightarrow\quad\sf{y-2=-3(x+1)}`

`\twoheadrightarrow\quad\sf{y-2=-3x-3}`

`\twoheadrightarrow\quad\sf{y=-3x-3+2}`

`\twoheadrightarrow\quad\sf{y=-3x-1}`

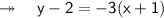
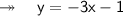
Therefore, the equation is y = -3x - 1.