Question

Kyle works at a donut​ factory, where a​ 10-oz cup of coffee costs 95¢​, a​ 14-oz cup costs​ $1.15, and a​ 20-oz cup costs​ $1.50. During one busy​ period, Kyle served 14 cups of​ coffee, using 204 ounces of​ coffee, while collecting a total of ​$16.70. How many cups of each size did Kyle​ fill?

Kyle filled ___ ​10-oz cup(s), ___ 14-oz cup(s), and ___ ​20-oz cup(s).

Answer 1

Kyle filled 4 10-oz cups, 5 14-oz cups, and 5 20-oz cups.

Step-by-step explanation:

Let's solve this problem step by step:

Let's assume that Kyle filled x 10-oz cups, y 14-oz cups, and z 20-oz cups.

From the information given, we can set up the following equations:

1. x + y + z = 14
2. 10x + 14y + 20z = 204
3. 0.95x + 1.15y + 1.5z = 16.70

Now, we can solve these equations simultaneously to find the values of x, y, and z.

Using a method of elimination or substitution, we find that x = 4, y = 5, and z = 5.

Therefore, Kyle filled 4 10-oz cups, 5 14-oz cups, and 5 20-oz cups.

Answer 2

Kyle filled 4 10-oz cups, 6 14-oz cups, and 4 20-oz cups.

Step-by-step explanation:

Let 10-oz, 14-oz, and 20-oz coffees be represented by the variables a, b, and c, respectively.

Since a total of 14 cups of coffee was served:

`a+b+c=14`

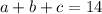
A total of 204 ounces of coffee was served. Therefore:

`10a+14b+20c=204`

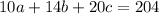
A total of $16.70 was collected. Hence:

`0.95a+1.15b+1.5c=16.7`

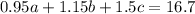
This yields a triple system of equations. In order to solve a triple system, we should isolate the system to only two variables first.

From the first equation, let's subtract a and b from both sides:

`c=14-a-b`

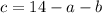
Substitute this into both the second and third equations:

`10a+14b+20(14-a-b)=204`

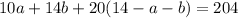
And:

`0.95a+1.15b+1.5(14-a-b)=16.7`

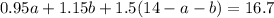
In this way, we've successfully created a system of two equations, which can be more easily solved. Distribute:

For the Second Equation:

`\displaystyle \begin{aligned} 10a+14b+280-20a-20b&=204\\ -10a-6b&=-76\\5a+3b&=38\end{aligned}`

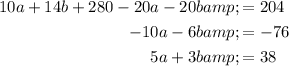
And for the Third:

`\displaystyle \begin{aligned} 0.95a+1.15b+21-1.5a-1.5b&=16.7\\ -0.55a-0.35b&=-4.3\end{aligned}`

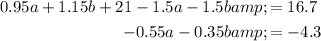
We can solve this using substitution. From the second equation, isolate a:

`\displaystyle a=(1)/(5)(38-3b)=7.6-0.6b`

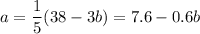
Substitute into the third:

`-0.55(7.6-0.6b)-0.35b=-4.3`

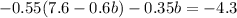
Distribute and simplify:

`-4.18+0.33b-0.35b=-4.3`

Therefore:

`-0.02b=-0.12\Rightarrow b=6`

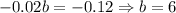
Using the equation for a:

`a=7.6-0.6(6)=4`

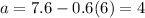
And using the equation for c:

`c=14-(4)-(6)=14-10=4`

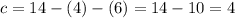
Therefore, Kyle filled 4 10-oz cups, 6 14-oz cups, and 4 20-oz cups.