Question

A -4.33 x 10⁻⁶ c charge is placed a certain distance from a -7.81 × 10⁻⁴ c charge. their electric potential energy is 44.9 j. how far apart are they?

Answer 1

The distance between the charges is approximately
`\(0.676 \, \text{m}\)`.

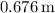The electric potential energy (U) between two charges can be calculated using the formula:

`\[ U = (k \cdot |q_1 \cdot q_2|)/(r) \]`

Where:

U = electric potential energy

k = Coulomb's constant
`(\(8.9875 * 10^9 \, \text{N m}^2/\text{C}^2\))`

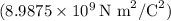
`\( q_1 \) and \( q_2 \)` = magnitudes of the charges

r = distance between the charges

Given:

`\( q_1 = -4.33 * 10^(-6) \, \text{C} \)`

`\( q_2 = -7.81 * 10^(-4) \, \text{C} \)`

`\( U = 44.9 \, \text{J} \)`

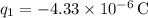
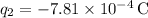
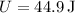
We can rearrange the formula to solve for the distance ( r ) between the charges:

`\[ r = (k \cdot |q_1 \cdot q_2|)/(U) \]`

Substitute the known values:

`\[ r = \frac{8.9875 * 10^9 \, \text{N m}^2/\text{C}^2 \cdot |(-4.33 * 10^(-6)) \cdot (-7.81 * 10^(-4))|}{44.9 \, \text{J}} \]`

Calculate the distance ( r ):

`\[ r \approx (8.9875 * 10^9 \cdot 3.38 * 10^(-9))/(44.9) \]`

`\[ r \approx (3.038 * 10^1)/(44.9) \]`

`\[ r \approx 0.676 \, \text{m} \]`

Answer 2

The distance apart of the two charges, given that their electric potential energy is 44.9 J, is 0.68 m

How to calculate the distance apart of the charges?

The following were analyzes from the above question:

• Charge of first object (Q₁) =
  `4.33*10^(-6)\ C`
• Charge of second object (Q₂) =
  `7.81*10^(-4)\ C`
• Electrical constant (K) =
  `9*10^(9)\ Nm^2/C^2`
• Electric potential energy (U) = 44.9 J
• Distance apart (r) = ?

The distance apart of the two charges can be calculated as illustrated below:

`U = (KQ_1Q_2)/(r) \\\\Thus,\\\\r = (KQ_1Q_2)/(U) \\\\r = (9*10^(9)\ *\ 4.33*10^(-6)\ *\ 7.81*10^(-4))/(44.9)\\\\r = 0.68\ m`

Thus, the distance apart of the charges is 0.68 m