Question

A sample of a radioactive isotope had an initial mass of 540 mg in

the year 2009 and decays exponentially over time. A measurement
in the year 2011 found that the sample's mass had decayed to 300
mg. What would be the expected mass of the sample in the year
2021, to the nearest whole number?

Answer 1

16 mg

Explanation:

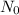`N_0` = Initial mass of sample = 540 mg

t = Time taken = 2 years

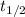`t_(1/2)` = Half life of isotope

N = Final mass of sample = 300 mg

Radioactive decay is given by

`N=N_0e^{-(\ln 2)/(t_(1/2))t}\\\Rightarrow \ln(N)/(N_0)=-(\ln 2)/(t_(1/2))t\\\Rightarrow t_(1/2)=-(\ln2)/(\ln(N)/(N_0))t\\\Rightarrow t_(1/2)=-(\ln2)/(\ln(300)/(540))2\\\Rightarrow t_(1/2)=2.358\ \text{years}`

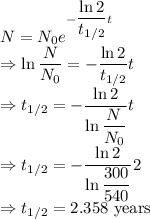
In 2021 the number of years passed from 2009 would be 12 years

`N=N_0e^{-(\ln 2)/(t_(1/2))t}\\\Rightarrow N=540e^{-(\ln 2)/(2.358)12}\\\Rightarrow N=15.86\approx 16\ \text{mg}`

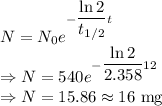
The expected mass of the sample in the year 2021 would be 16 mg.