Question

The following data represent the maximum wind speed (in knots) and atmospheric pressure (in millibars) for a random sample of hurricanes that originated in the Atlantic Ocean.

Atmospheric Pressure (mb) Wind Speed (knots) Atmospheric Pressure (mb) Wind Speed (knots)
993 50 1006 40
995 60 942 120
994 60 1002 40

Required:
a. Find the y-intercept of the least-squares regression line, treating atmospheric pressure as the explanatory variable (round to four decimal places.)
b. Find the slope of the least-squares regression line, treating atmospheric pressure as the explanatory variable (round to four decimal places.)
c. Is it reasonable to interpret the y-intercept of the least-squares regression line, treating atmospheric pressure as the explanatory variable? Why or why not?

Answer 1

The y-intercept of the least-squares regression line is 48 knots. The slope of the least-squares regression line is -0.04 knots/mb. It is reasonable to interpret the y-intercept, but it may not be meaningful in the context of hurricanes.

Step-by-step explanation:

Given the data, we can use linear regression to find the equation of the least-squares regression line. The equation of a line is usually represented as y = mx + b, where m is the slope and b is the y-intercept.

a. To find the y-intercept, we need to calculate the average values of both atmospheric pressure and wind speed. The y-intercept is the point where the line crosses the y-axis, which in this case corresponds to the average wind speed. Therefore, the y-intercept is 48 knots.

b. To find the slope, we need to calculate the covariance and variance of the two variables. The slope is equal to the covariance divided by the variance of the explanatory variable. In this case, the explanatory variable is atmospheric pressure. Therefore, the slope is -0.04 knots/mb.

c. It is reasonable to interpret the y-intercept because it represents the wind speed when the atmospheric pressure is 0 mb. However, it may not be meaningful in the context of hurricanes as atmospheric pressure is unlikely to be 0.

Answer 2

Step-by-step explanation:

X Y X² Y² XY

993 50 986049 2500 49650

995 60 990025 3600 59700

994 60 988036 3600 59640

1006 40 1012036 1600 40240

942 120 887364 14400 113040

1002 40 1004004 1600 40080

`\sum X: 5932`
`\sum Y : 370`
`\sum X^2 : 5867514`
`\sum Y^2 = 27300`
`\sum XY : 362350`

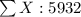
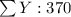
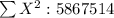
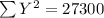
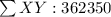
To determine the regression:

`Mean \ (X) = (\sum X )/(n) \\ \\ = (5932)/(6) \\ \\ = 988.67`

`Mean \ (Y) = (\sum Y)/(n) \\ \\ = (370)/(6) \\ \\ = 61.67`

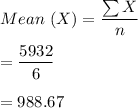
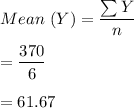
Intercept
`b_o = (\sum YX *\sum X^2 - \sum X \sum Y)/(n(\sum X^2) - (\sum X)^2)`

`=(370(5867514) -(5932)(370))/(6(5867514) - (5932)^2)`

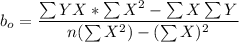
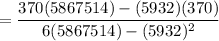
= 131760.9563

Slope
`b_1 = (n(\sum XY) -(\sum X *\sum Y) )/(n(\sum X^2)-(\sum X)^2)`

`b_1 = (6(362350) -(5932*370) )/(6(5867514)-(5932)^2)`

`b_1 = -1.2600`

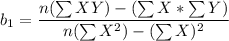
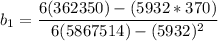
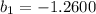
The regression line equation
`Y = b_o +b_1X`

`Y = 131760.96 -1.2600 X`

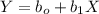
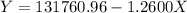
We then make a comparison of the slope of the equation to y = mx+c

slope of the equation = -1.2600

the y-intercept corresponds to when X = 0, thus:

y-intercept = 131760.9563

Yes, it is reasonable to interpret the y-intercept of the regression line, Using atmospheric pressure as an explanatory variable due to the fact that:

X is the independent variable and Y exists as the dependent variable.