Answer:
Step-by-step explanation:
X Y X² Y² XY
993 50 986049 2500 49650
995 60 990025 3600 59700
994 60 988036 3600 59640
1006 40 1012036 1600 40240
942 120 887364 14400 113040
1002 40 1004004 1600 40080
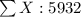
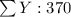
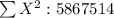
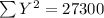
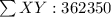
To determine the regression:
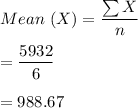
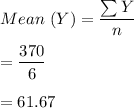
Intercept
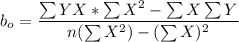
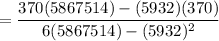
= 131760.9563
Slope
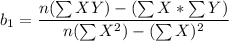

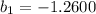
The regression line equation

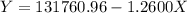
We then make a comparison of the slope of the equation to y = mx+c
slope of the equation = -1.2600
the y-intercept corresponds to when X = 0, thus:
y-intercept = 131760.9563
Yes, it is reasonable to interpret the y-intercept of the regression line, Using atmospheric pressure as an explanatory variable due to the fact that:
X is the independent variable and Y exists as the dependent variable.