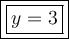Answer:
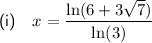

Explanation:
Question (i)
Given equation:
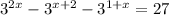
Apply exponent rules to rewrite each term on the left side of the equation in terms of
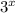 :
:
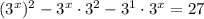
Factor out
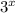 :
:
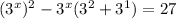
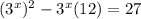
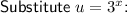
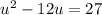
Subtract 27 from both sides to create a quadratic equation in the form ax² + bx + c = 0:
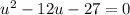
Solve the equation for u using the quadratic formula.

In this case:
Therefore:
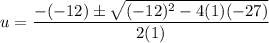
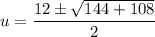
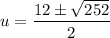
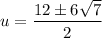
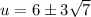
Substitute back
 and solve for x.
and solve for x.
Solution 1
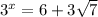
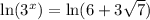
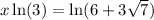
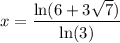
Solution 2
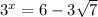
As
 , and
, and
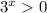 , there are no solutions for x ∈ R.
, there are no solutions for x ∈ R.
Therefore, the only valid solution to the given equation is:


Question (ii)
Given equation:
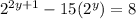
Apply exponent rules to rewrite each term on the left side of the equation in terms of
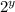 :
:
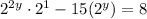

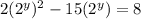
Subtract 8 from both sides:
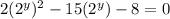

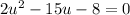
Factor the quadratic equation:
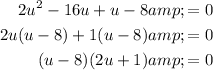
Solve for u:
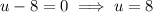
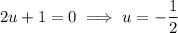
Substitute back
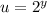 and solve for y.
and solve for y.
Solution 1
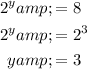
Solution 2
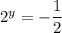
As
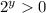 , there are no solutions for y ∈ R.
, there are no solutions for y ∈ R.
Therefore, the only valid solution to the given equation is: