Question

B) If the volume of a cube is 125 cm³, (i) find its length (ii) Find its total surface area

​

Answer 1

(i) side = 5 cm

(ii) SA = 150 cm²

Explanation:

(i)

V = s³

`s = \sqrt[3]{V}`

`s = \sqrt[3]{125~cm^3}`

`s = 5~cm`

The side of the cube measures 5 cm.

(ii)

The cube has 6 faces. The faces are congruent squares with side 5 cm.

SA = 6 × s²

SA = 6 × (5 cm)²

SA = 150 cm²

Answer 2

The length of the cube is 5 cm.

The total surface area of the cube is 150 cm².

Explanation:

Given that:

`\sf \textsf{ The volume of a cube}= 125 cm^3`

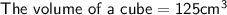
We can find the length of the cube by using the formula:

`\sf \textsf{Volume of cube }= length ^3`

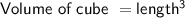
Substitute the value volume, we get:

`\sf 125 cm^3 = length^3`

Taking the cube root of both sides, we get:

`\sf length = \sqrt[3]{125} cm`

`\sf length = 5 cm`

Therefore, the length of the cube is 5 cm.

The total surface area of a cube can be found using the formula:

`\sf \textsf{ Total Surface Area of cube}= 6 * length^2`

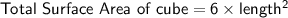
Substitute the value of length, we get:

`\sf \textsf{ Total Surface Area of cube}= 6 * 5^2`

`\sf \textsf{ Total Surface Area of cube}= 6 * 25`

`\sf \textsf{ Total Surface Area of cube}= 150 cm^2`

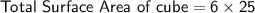
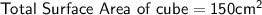
Therefore, the total surface area of the cube is 150 cm².