Question

1796.4 was my final answer but it says its wrong, i dont understand this whatsoever, i did subtracting and squaring but i guess im too not smart know the answer for this

ill pay pal $100 to whoever finishes my chem class

Answer 1

Variance (σ²) = 1497

Explanation:

To find the variance of a set of data, we can use the following formula:

`\large\boxed{\displaystyle \text{Variance},\; \sigma^2=(\sum x^2)/(n)-\overline{x}^2}`

where:

• 
  `x`-values are the data.
• 
  `n` is the number of data points in the set.
• 
  `\overline{x}` is the mean (average) of the data set.

Given:

• Data points: 95, 80, 191, 86, 122, 86
• Mean
  `\overline{x} = 110`

Substitute the values into the formula:

`\begin{aligned}\displaystyle \text{Variance},\; \sigma^2&=(95^2+80^2+ 191^2+86^2+122^2+86^2)/(6)-110^2\\\\&=(9025+6400+36481+7396+14884+7396)/(6)-12100\\\\&=(81582)/(6)-12100\\\\&=13597-12100\\\\&=1497\end{aligned}`

Therefore, the variance of the given data set is 1497.

Answer 2

`\sf \sf Variance \left[\sigma^2\right]=\boxed{\sf 1497}`

Explanation:

Note:

In statistics, Variance is a measure of how much the values in a data set vary or spread out from the mean (average).

It quantifies the degree to which individual data points deviate from the average.

In order to calculate the variance of the given data, we can use the formula:

`\sf \sigma^2 = \frac{\sum_(i=1)^(n)(x_i - \overline{x})^2}{n}`

where

`\textsf{ $\sigma^2$ is the variance, }`

`\textsf{ $\sf x_i$ is the $\sf i^(th)$ data point,}`

`\textsf{$\sf\overline{x} $ is the mean of the data, and}`

`\textsf{ $\sf n$ is the number of data points.}`

`\hrulefill`

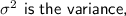
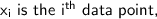
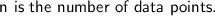
In this case:

`\sf data=95, 80, 191, 86, 122, 86`

`\sf mean(\overline{\sf x}) = 110`

`\sf \textsf{ number of data(n) }= 6`

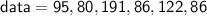
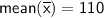
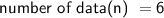
Therefore, we can calculate the variance as follows:

`\sf \sigma^2 = ((95-110)^2 + (80-110)^2 + (191-110)^2 + (86-110)^2 + (122-110)^2 + (86-110)^2)/(6)`

`\sf \sigma^2 = ((-15)^2 + (-30)^2 + (81)^2 + (-24)^2 + (12)^2 + (-24)^2)/(6)`

`\sf \sigma^2 = (225 + 900 + 6561 + 576 + 144 + 576)/(6)`

`\sf \sigma^2 = (8982)/(6)`

`\sf \sigma^2 = 1497`

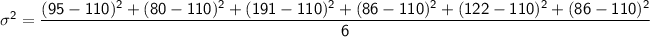
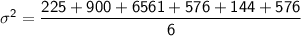
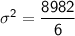
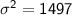
Therefore, the variance of the given data is 1497.