a. Let's denote the base of the triangle as
 (which is given as 4 inches) and the height a
(which is given as 4 inches) and the height a
 . The formula for the area of a triangle is
. The formula for the area of a triangle is
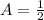 ×
×
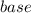 ×
×
 .
.
Given that the area
 is no more than 10 square inches, we can write the inequality as:
is no more than 10 square inches, we can write the inequality as:
 ×
×
 ×
×

Since the base
 is given as 4 inches, the inequality becomes:
is given as 4 inches, the inequality becomes:
 ×
×
 ×
×

Simplifying:
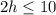
b. Now we can solve for
 :
:
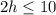
Divide both sides by 2:
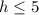
So, the maximum height
ℎ
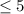
h of the triangle is 5 inches.
c. Given the dimensions of the triangle, which are a base of 4 inches and a height of 5 inches, the maximum height of the triangle is 5 inches. This matches the result obtained from solving the inequality in part B.