Question

How much must be deposited today into the following account in order to have a $135,000 college fund in 14 years? Assume no additional deposits are made. An account with annual compounding and an APR of ​ 5 . 7 %

Answer 1

$62,127.51

Explanation:

To find out how much must be deposited today into an account with a 5.7% APR compounded annually to achieve a balance of $135,000 in 14 years, we can use the compound interest formula.

Compound Interest Formula

`\large \text{$ \sf A=P\left(1+(r)/(n)\right)^(nt) $}`

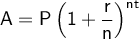
where:

• A is the account balance.
• P is the principal amount invested.
• r is the interest rate (in decimal form).
• n is the number of times interest is applied per year.
• t is the time (in years).

In this case:

• A = $135,000
• r = 5.7% = 0.057
• n = 1 (annually)
• t = 14 years

Substitute the given values into the formula and solve for P:

`\sf 135000=P\left(1+(0.057)/(1)\right)^(1 * 14)`

`\sf 135000=P\left(1+0.057\right)^(14)`

`\sf 135000=P\left(1.057\right)^(14)`

`\sf 135000=P(2.1729504456...)`

`\sf P=(135000)/(2.1729504456...)`

`\sf P=62127.50975...`

`\sf P=62127.51\; (2\;d.p.)`

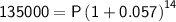
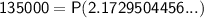
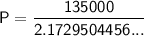
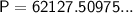
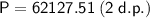
Therefore, the amount that must be deposited is $62,127.51 (rounded to the nearest cent).