Answer:
Part a: David's pattern is an example of inductive reasoning.
Part b: Yes, David's conclusion is correct.
Explanation:
- Inductive reasoning is a type of reasoning that draws a general conclusion from specific observations.
It is based on the assumption that if something is true in a few cases, it is likely to be true in all cases. - Deductive reasoning is a type of reasoning that moves from general principles to a specific conclusion.
It is based on the assumption that if the premises are true, then the conclusion must also be true.
Part a:
Inductive reasoning is a type of reasoning that draws a general conclusion from specific observations.
In this case,
David observed a pattern in the three examples he provided and then generalized that any two-digit number ending in 9 can be expressed as:

where n is the tens of the number.
So,
David's pattern is an example of inductive reasoning.

Part b:
We can verify this by testing it with a few examples.
For instance, let's consider the two-digit number 59.
The tens digit of 59 is 5.
Therefore, according to David's formula,
We should have:
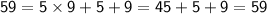
This is indeed true.
We can also test this formula with other two-digit numbers ending in 9 and we will find that it holds true for all such numbers.
Therefore, we can conclude that David's formula is correct for any two-digit number ending in 9.